-
 @ david
2024-08-31 20:23:59
@ david
2024-08-31 20:23:59The GrapeRank algorithm, like the PageRank algorithm, takes as input a graph, composed of nodes and edges, and composes "importance" scores for each node based on the topology of the graph. This equation is currently implemented at brainstorm and uses follows and mutes to calculate a trust score G (also called an "influence" score) in the range [0, 1] for each user in your nostr network.
This is the GrapeRank equation:
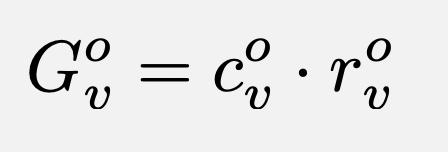
- G, c, and r in this equation are each scalars in the interval [0, 1]
- G represents the grapevine score (also called the "influence") of v, as seen from the vantage point of o
- r represents the average rating of v by o's grapevine
- c represents the degree of confidence in the average rating r
- the subscript always represents the thing (user, product, etc) being evaluated
- the superscript always represents the "observer," the point of reference from which we view and interpret the world
This is the same equation in expanded format:
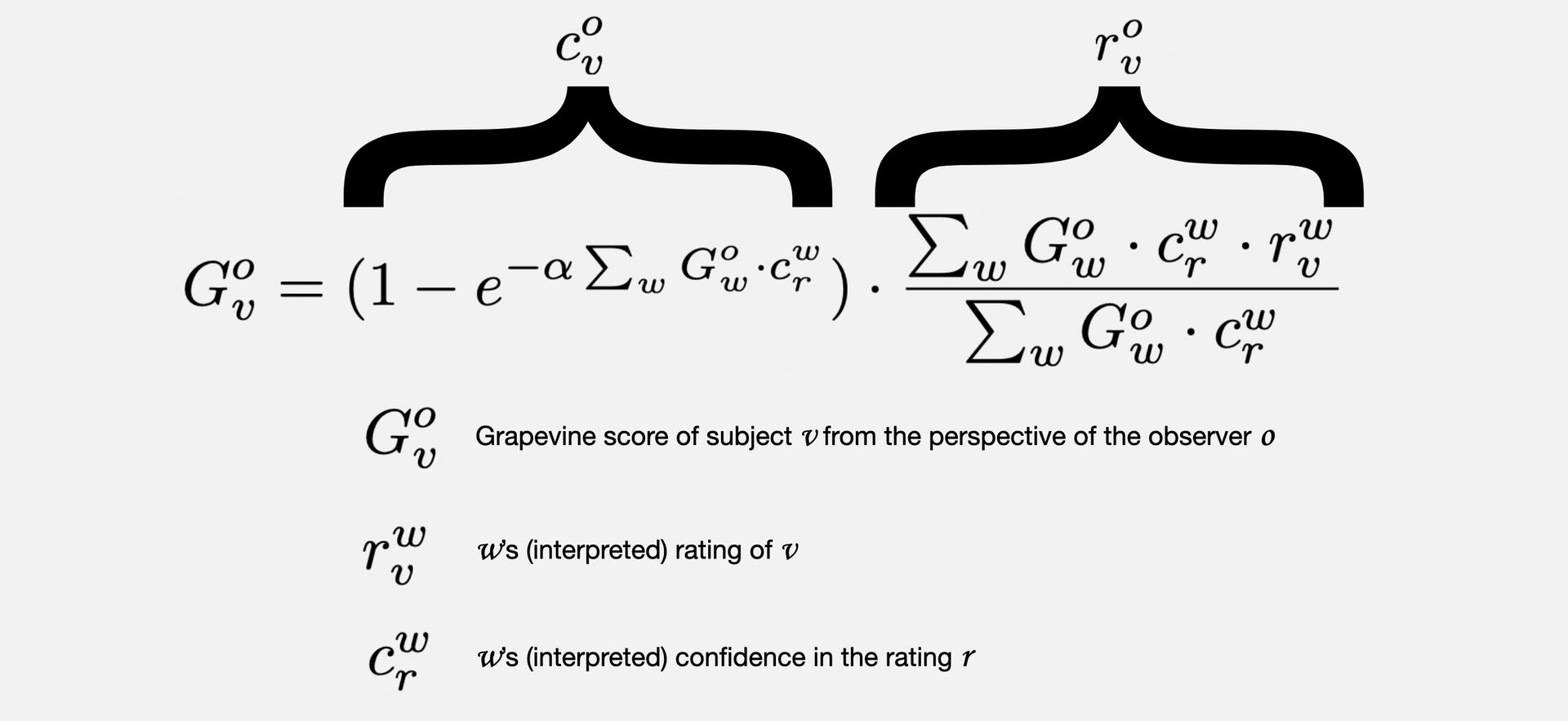
- The grapevine score of v on the left, G_v, is weighted using the grapevine score (but of each w) on the right, G_w
- These calculations are iterated until all G values converge
- r^o_v (the right half) is the weighted average
- c^o_v (the left half) is the confidence in that weighted average
- The r^w_v are the ratings being averaged together; they are inferred from follows and mutes by interpreting a follow as a score of 1 (probably not a bot), a mute as a score of 0 (probably a bot)
- The c^w_r are the confidences in the r^w_v; a follow is interpreted to have a confidence of 5 percent, a mute to have a confidence of 10 percent. (These are adjustable settings at brainstorm.)
- The sum over G * c, which appears twice in the above equation, is called the "input" and is an unbounded, nonnegative scalar which represents "the amount of trusted input" that goes into the calculation
- The formula is designed so that as the input (the number of ratings from trusted sources) increases to infinity, the confidence c^o_v approaches 1 (100 percent) asymptotically. This map from input onto confidence, which employs a nonlinear equation, is necessary to ensure that G remains within the [0, 1] interval even as input increases to infinity.
- alpha is a nonnegative scalar value that determines how "quickly" the confidence c^o_v approaches 1 (100 percent) as trusted input increases. Decreasing the value for alpha makes the equation more "rigorous" because it will take more trusted input to achieve any given degree of confidence. (Alpha is another user-adjustable setting at brainstorm.)
To perform the above calculations: 1. For the "seed" user (the observer o, i.e. the logged-in user), fix average, confidence, and G (influence) to unity. These values will not change. 2. For all other users, initialize average, confidence, and influence scores to zero. 3. Iterate through all users to calculate average, confidence, and influence scores. In the first iteration, the follows of the logged-in users will obtain nonzero scores. In the second iteration, their follows will obtain nonzero scores. And so on. 4. Continue iteration until all values converge.
Intuition tells us that convergence is guaranteed by the requirement that for each rating, the rating and its associated confidence are scalar values between 0 and 1. G will therefore also always also be a number between 0 and 1. Not shown: at brainstorm and in general recommended practice, the above equation also employs a scalar value between 0 and 1 called the "attenuation factor," defaulted at 0.8 but adjustable by the user, which causes influence scores G^o_v to diminish as the number of hops between o and v increases.
Intended usage
G is designed to be used as a weight when calculating weighted averages, tallying votes, etc. It is highly effective at eliminating bots without turning into a popularity contest.
Interpretation
G^o_v is a recommendation, to you by your grapevine, that reflects in numerical form how much "attention" you should pay to pubkey v in the given context (if a context is given).
- G^o_v = 0 means that pubkey v is not worthy of your attention, because v is probably a bot
- G^o_v = 1 means that pubkey v is worthy of your full attention, because b is probably not a bot
- Values between 0 and 1 mean the grapevine isn't absolutely certain one way or another, whether because of scant information (some follows by trusted sources, but not many) or conflicting information (combination of follows and mutes)
Note that if a bad actor spins up a large number of bots and uses them to follow himself, those follows will be completely ignored, because those bots will have a zero trust score G.
Change of context
The set of ratings r can be generated from any data source, regardless of format. By selecting different ratings datasets, we can generate grapevine scores to reflect different contexts. Example: collect emoji reactions to content on Topic X and infer a fire emoji as a rating of 2, rocket as a 3, thumb down as a 0, etc. The resulting G, which will take values between 0 and 3, is now interpreted to apply only to Topic X.
Compact notation
The above equation can be written more succinctly:
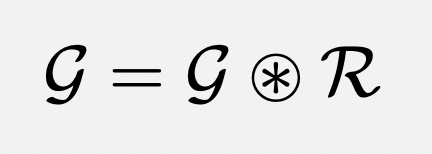
where G represents the baseline grapevine score, and R represents the dataset generated from follows and mutes.
Note that we can use a different G on the left versus on the right:
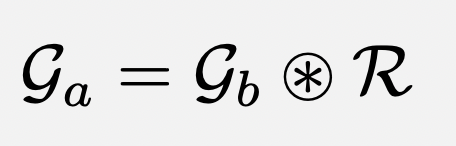
The same relationship can be expressed using arrow notation:
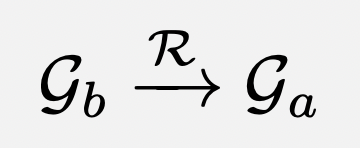
The above relationship in arrow notation should be read to mean that the set of scores G_a are calculated using dataset R which has been authored exclusively by members represented by G_b. In other words, the ratings R are weighted using the set of scores G_b.
Note that the dataset R is generated via interpretation of preexisting content. We can use any content that we can find. There is no requirement or expectation that users will necessarily generate ratings in a format convenient for input into the grapevine. The process of "interpretation" takes care of that, by "translating" existing data into a format suitable for use by the grapevine.
Note also that grapevine scores G may refer to anything in any context: trust scores for users, quality scores for products, etc.
Concerns about convergence
If the G_a and G_b represent the same context (G_a = G_b), the relationship is said to be "recursive," and calculations are iterated until they converge.
If G_a != G_b, the relationship is not recursive, and a single iteration through each pubkey is all that is needed. This means that we can allow G_a and / or G_b to be greater than 1 with no need to worry about convergence.
Worldviews
Arrow notation allows us to link trust calculations in chains:

A graph of grapevine scores G_i linked via arrow notation is called a worldview.
For example, consider the following worldview: * G_a is the baseline nostr trust score, as described above, intended to separate bots from real users * G_b is a label applied to nostr users, intended as a label for bitcoiners (as opposed to nocoiners or shitcoiners) * G_c is a quality score applied to hardware wallets
The purpose of the above worldview is so that I can get a ranked list of hardware wallets and I can be reasonably sure that the list is curated by bitcoiners whose instincts on this topic I value more highly than the general population.
Worldviews can contain any desired number of nodes, connected by any desired number of arrows, and so can be as complex as desired.
Obviously, the construction of a worldview reflects the value system of the person who uses it, with the above worldview offered as a reflection of maximalist values and beliefs. Worldviews can be codified and submitted to the wider community. One's grapevine can even be used to select individuals who should be trusted to edit or construct worldviews.
Computational cost
The methods described above are expected to be too time consuming and computationally expensive to do all of them on the fly on the front end. Notably, the ones that are recursive. Non-recursive computations, however, can be done on the front end, provided recursive calculations have been done ahead of time and are readily available. It is anticipated that the value added by well-crafted worldviews will more than justify the requisite costs.